 б)
б) 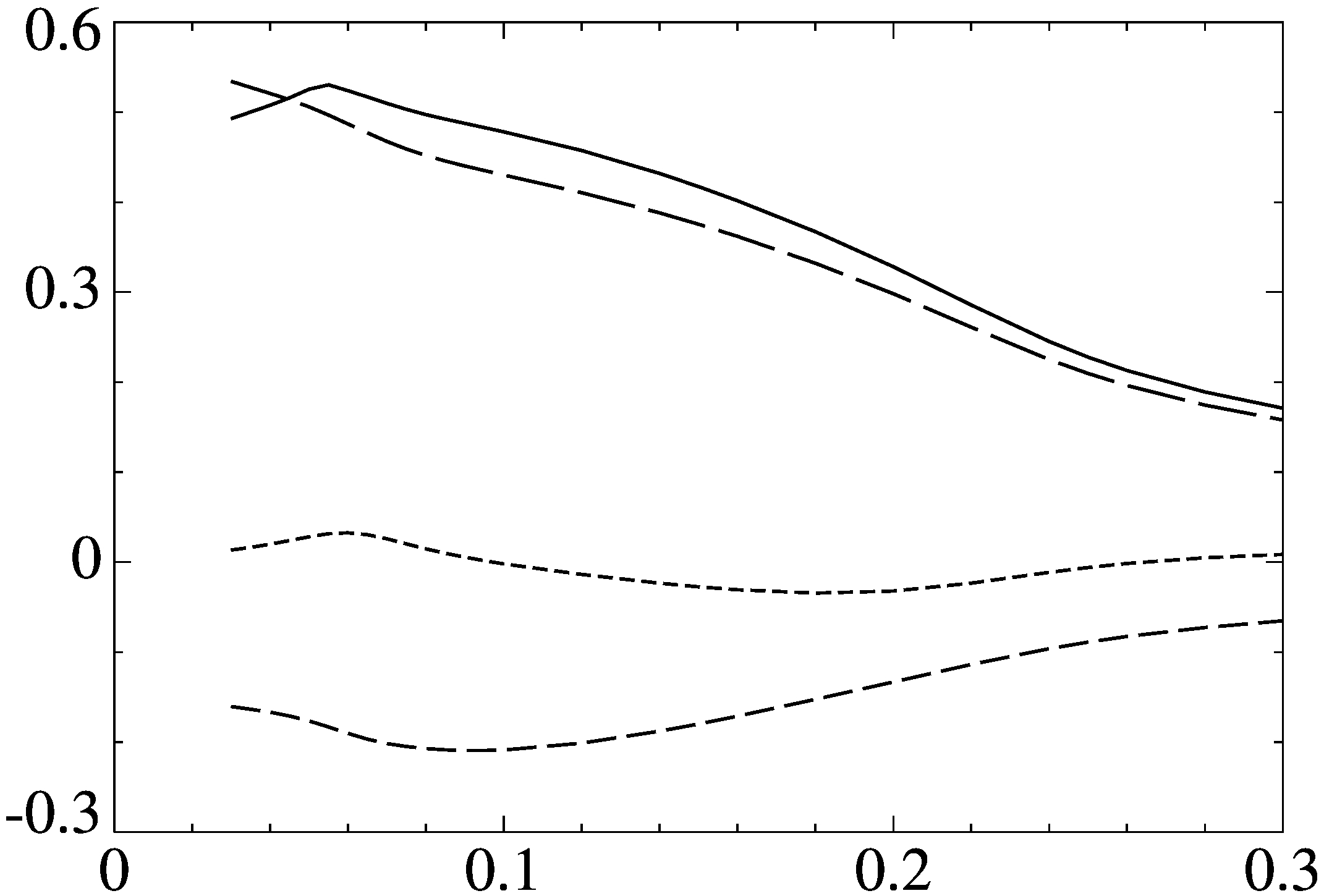
Рассмотрена кинематическая генерация пространственно-периодическим течением электропроводной жидкости магнитных мод вида произведения трехмерного поля, имеющего такую же периодичность, на гармонику Фурье с произвольным постоянным волновым вектором q. Проведены расчеты магнитных мод с максимальным по q инкрементом роста ? для модельного течения общего вида (в таких течениях присутствует магнитный ?-эффект) и для центрально-симметричного модельного течения (в таких течениях ?-эффект отсутствует, но в модельном течении присутствует отрицательная магнитная вихревая диффузия). Показано, что магнитные моды с максимальным по q инкрементом роста ? характеризуются слабым разделением пространственных масштабов, поэтому указанные эффекты не могут считаться основными механизмами их генерации.
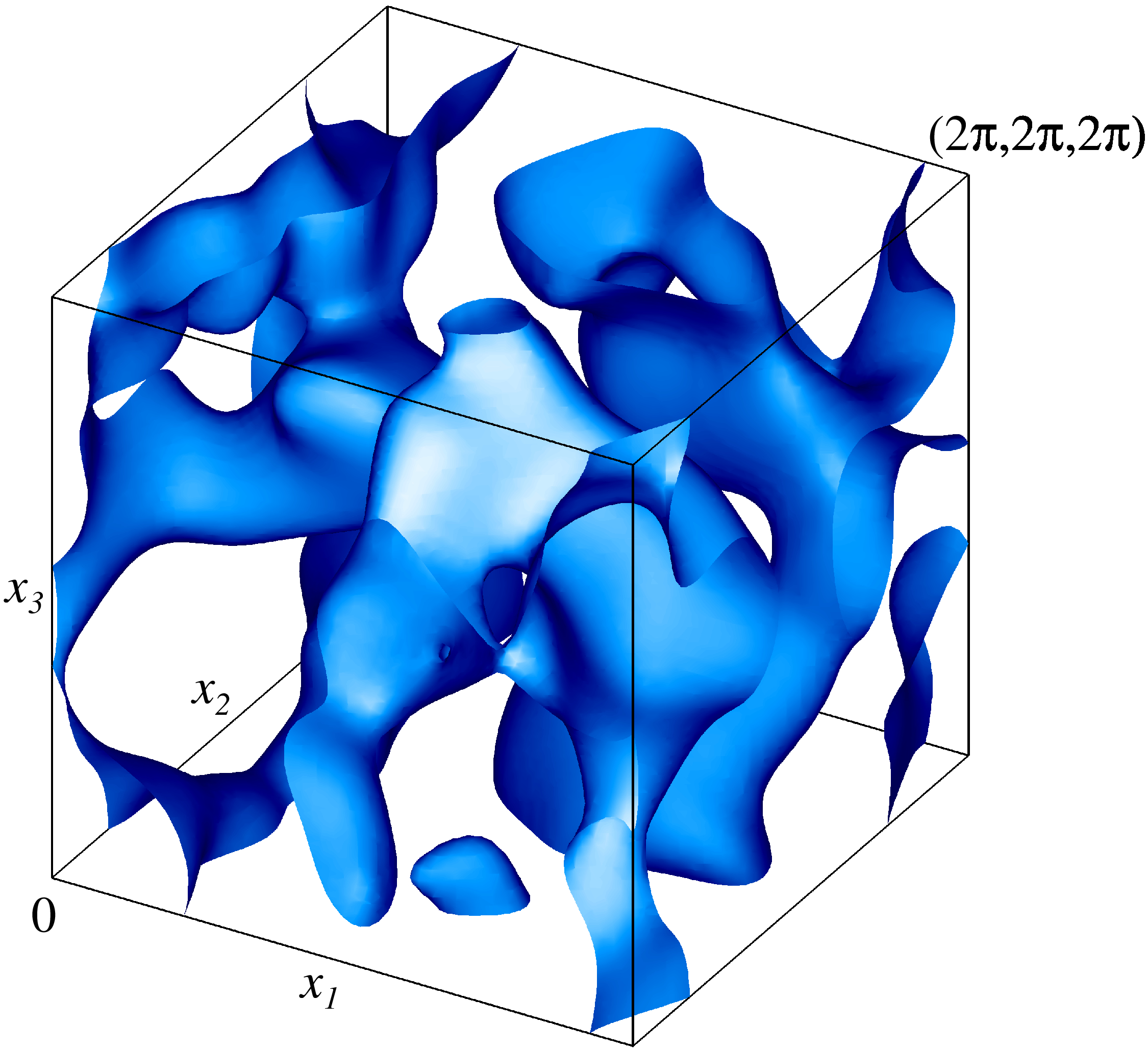
Изоповерхности плотности кинетической энергии модельного течения общего вида на уровне 50% от максимальной плотности. Изображен один куб периодичности течения.
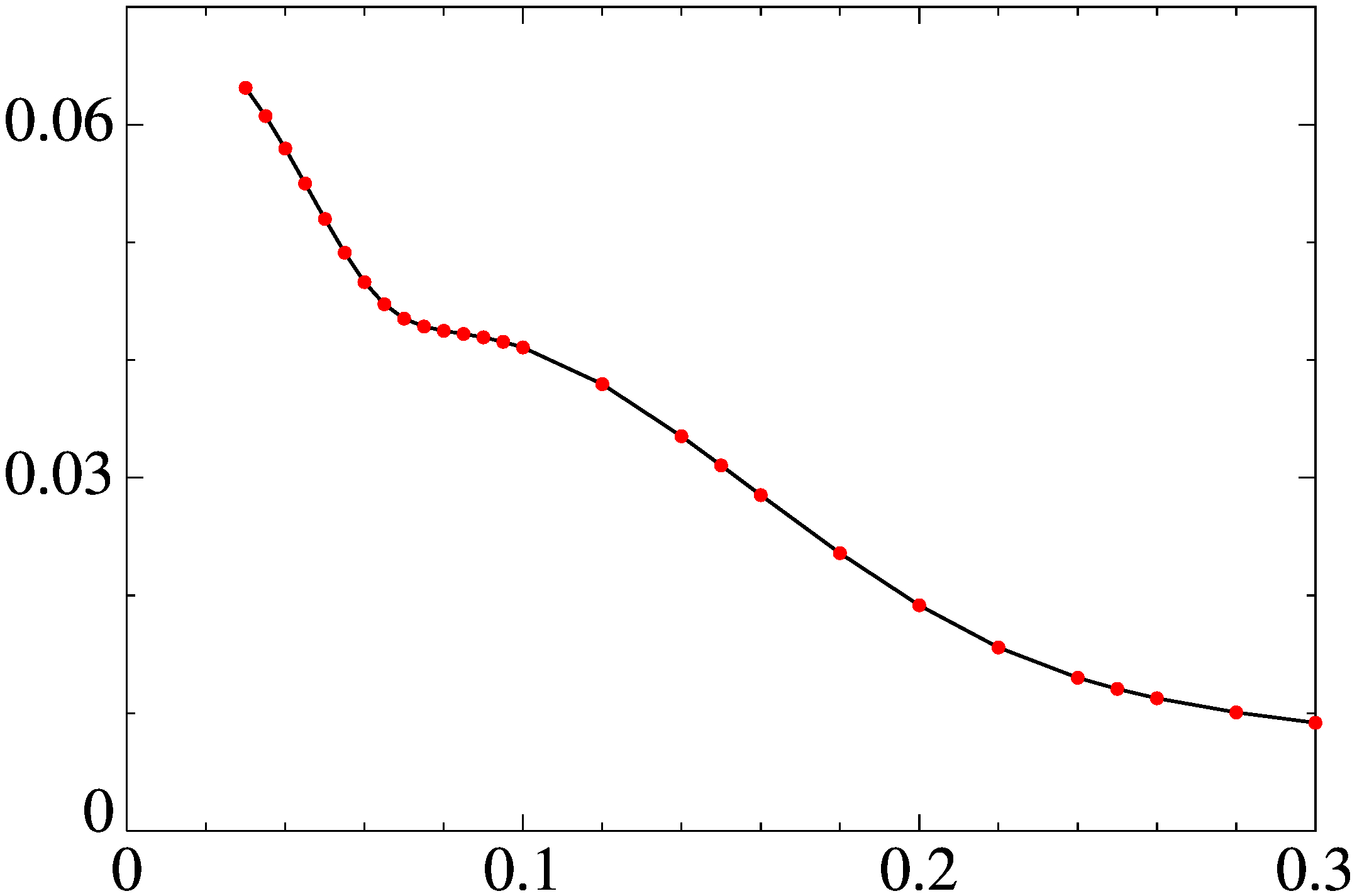
Максимальный по q инкремент роста магнитных мод ? (вертикальная ось) (а) для модельного течения общего вида и волновой вектор q (вертикальная ось) (б), для которого достигается maxq?, как функции молекулярной магнитной диффузии ? (горизонтальная ось). Точки показывают вычисленные величины maxq? (а). Сплошная линия: |q|, штриховые: qn, длина штриха увеличивается с индексом n (б).
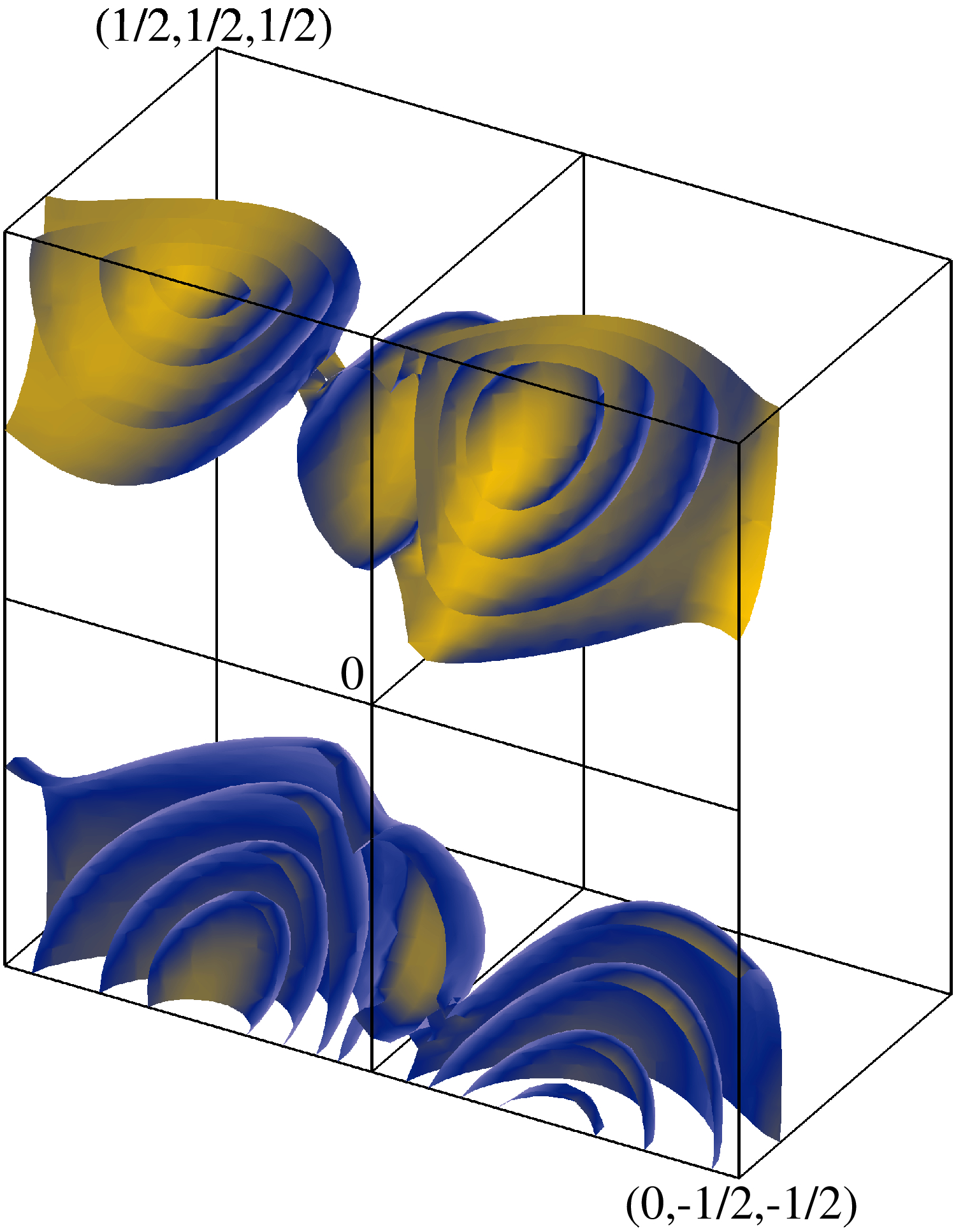
Изоповерхности инкремента ? в пространстве волновых векторов q для модельного течения общего вида для молекулярной магнитной диффузии ?=0.1 на уровнях 25%, 50%, 75% и 90% от maxq?.
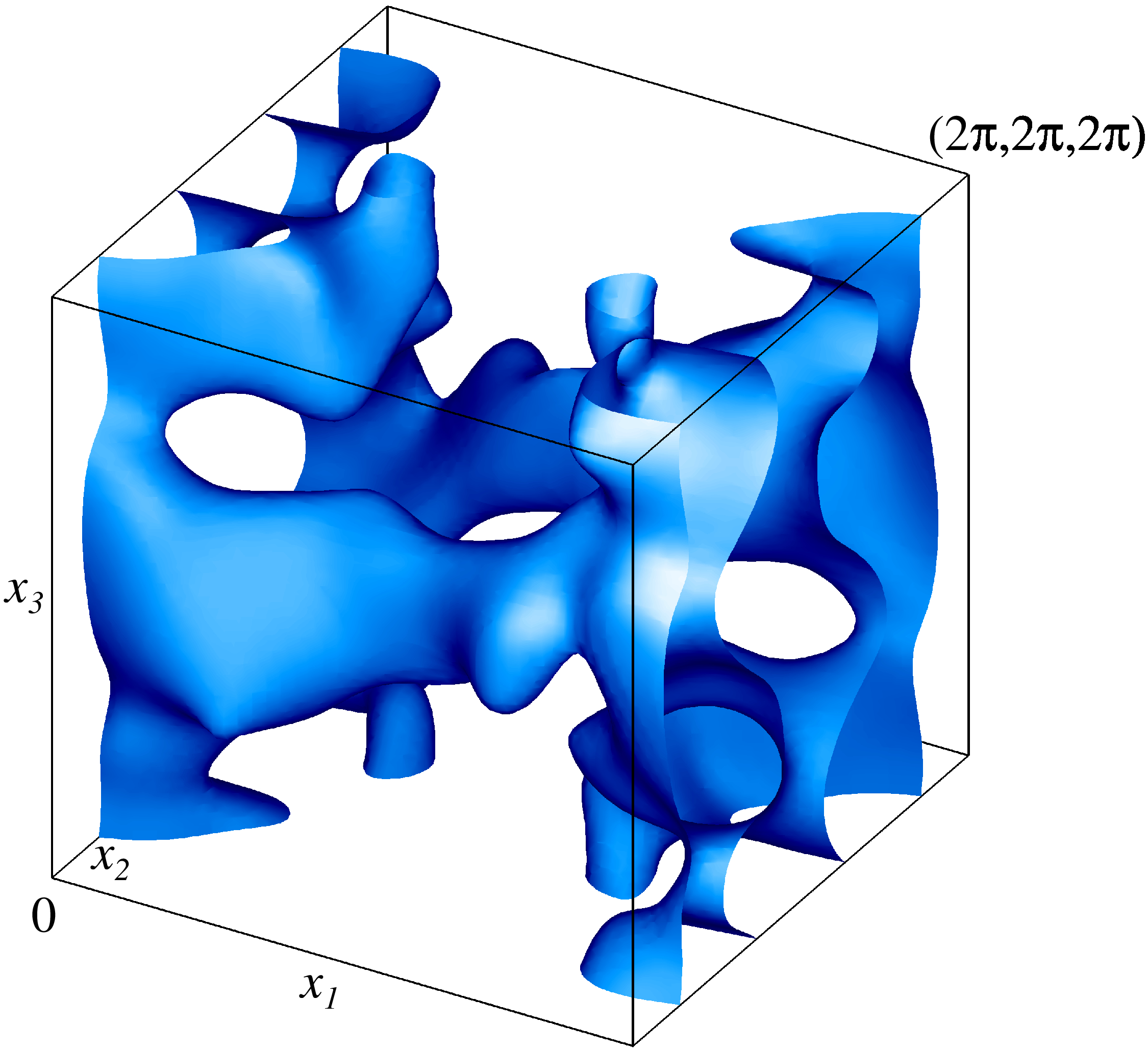
Изоповерхности плотности кинетической энергии центрально-симметричного модельного течения на уровне 60% от максимальной плотности. Изображен один куб периодичности течения.
Максимальный по q инкремент роста магнитных мод g (вертикальная ось) (а) для центрально-симметричного модельного течения и волновой вектор q (вертикальная ось) (б), для которого достигается maxq?, как функции молекулярной магнитной диффузии h (горизонтальная ось). Точки показывают вычисленные величины maxq? (а). Локальные максимумы ? достигаются при q=0 (правая ветвь, пунктир, нейтральные моды), q=(0,1/2,0) (средняя ветвь, штриховая линия), для левой ветви (сплошная линия) соответствующие q изображены на графиках (б): сплошная линия: |q|, штриховые: qn, длина штриха увеличивается с индексом n (б).
Изоповерхности инкремента роста ? магнитных мод в пространстве волновых векторов q для центрально-симметричного модельного течения общего вида для молекулярной магнитной диффузии ?=0.1 на уровнях 25%, 50%, 75% и 90% от maxq?.
Публикации: