В журнале «Zeitschrift für angewandte Mathematik und Physik» (WoS, Scopus, Q1) издательства Springer вышла статья «A boundary value problem in the theory of elasticity for a rectangle: exact solutions». Среди авторов — сотрудники ИТПЗ РАН: ведущий научный сотрудник, д.ф.-м.н. М.Д. Коваленко, старший научный сотрудник, к.ф.-м.н. И.В. Меньшова и старший научный сотрудник, к.ф.-м.н. А.П. Кержаев.
В статье получены формулы, описывающие точное решение краевой задачи теории упругости в прямоугольнике, у которого две противоположные (горизонтальные) стороны свободны, а на двух других (торцах прямоугольника) заданы напряжения. Рассмотрены все случаи симметрии относительно центральных осей, комбинируя которые можно получить решения, не обладающие симметрией. Приводятся также формулы для полуполосы. Решения представляются в виде рядов по собственным функциям Папковича–Фадля, коэффициенты которых определяются по простым формулам.
Исследование выполнено при поддержке Российского научного фонда (проект № 19-71-00094) и Российского фонда фундаментальных исследований совместно с Китайским научным фондом (проект № 20-51-53021).
Точное решение краевой задачи в прямоугольнике с теми или иными граничными условиями на его сторонах, пожалуй, одна из наиболее известных проблем теории упругости на протяжении многих десятилетий. Ей посвящены сотни публикаций. Интерес к этой задаче обусловлен, в первую очередь, вопросами теоретического характера, такими как влияние концевых эффектов, поведение решений в окрестности угловых точек границы (например, можно ли решение для бесконечного клина рассматривать как асимптотическое в соответствующих задачах для прямоугольника?), оценка различных приближенных теорий (в частности, балочной) и т.д. Решение задачи для прямоугольника открывает путь к решению важных прикладных задач: передача сосредоточенных нагрузок к тонкому листу через ребра жесткости, неоднородные и температурные задачи, задачи с трещинами в прямоугольной области и т.п. Развитие аналогичных теорий в косоугольной и полярной системах координат позволили бы решить множество других задач (однородных, неоднородных, температурных). В косоугольной системе координат это решения для трапеции, треугольника, прямоугольника с «косой» трещиной и т.д. В полярной системе координат – решения для части кольца, для полуплоскости с круговыми выточками или отверстиями и т.д. Наконец, решение для прямоугольника лежит в основе точного решения классической трехмерной краевой задачи теории упругости для прямоугольного параллелепипеда.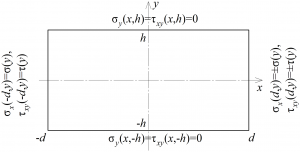
Значение точных решений трудно переоценить. В первую очередь потому, что они позволяют глубоко разобраться в физике изучаемого явления, ответить на вопрос об адекватности используемой математической модели исследуемому физическому явлению, оценить эффективность применения тех или иных приближенных или численных методов при решении сложных инженерных задач.
Статья базируется на теории разложений по собственным функциям Папковича–Фадля и преобразовании Бореля в классе квазицелых функций экспоненциального типа с вырожденной в отрезок (торцы прямоугольника) областью аналитичности.
Полученными формулами, строго говоря, описываются остаточные напряжения и те перемещения, которые возникают в результате их сброса с образованием разрывов. Поэтому изложение ведется с точки зрения остаточных напряжений. Для того чтобы перейти к решениям в классической постановке, надо определенным образом изменить знаки в формулах для перемещений или напряжений на противоположные.
Все формулы получены в предположении, что на стыках полуполос или прямоугольников, склеиваемых в бесконечную полосу с остаточными напряжениями, известны разрывы перемещений, возникающие при сбросе остаточных напряжений. Если же здесь известны напряжения, то нужно воспользоваться соответствующими формулами перехода, связывающими коэффициенты Лагранжа для перемещений и напряжений.
Источник: Kovalenko M.D., Menshova I.V., Kerzhaev A.P., Yu G. A boundary value problem in the theory of elasticity for a rectangle: exact solutions // Zeitschrift für angewandte Mathematik und Physik. 2020. V. 71. Article 199. DOI:10.1007/s00033-020-01425-2
