Бигармоническая проблема, ее решение и возможные приложения
Бигармоническая проблема – одна из интереснейших и популярнейших проблем математики и механики. В 2003 г. Мелешко В.В. опубликовал соответствующий обзор наиболее значимых (по мнению автора) публикаций, включающий список из более чем 700 наименований за почти 200 лет на практически всех европейских языках. Это был, наверное, последний обзор такого масштаба.
Сейчас трудно сказать, как впервые была сформулирована бигармоническая проблема: как математическая или как инженерная. Однако известно, что сначала она называлась «бигармонической проблемой теории упругости» и только позже, когда выяснилось, что с ее решением связаны и другие физические задачи, она стала называться просто «бигармонической проблемой».
С позиции инженера, занимающегося расчётами на прочность, суть бигармонической проблемы можно продемонстрировать на таком примере. Представим себе тонкую прямоугольную плиту, жёстко защемлённую по её сторонам, под действием некоторого внешнего нормального давления (например, сосредоточенной силы, приложенной в её центре – наиболее яркая задача). Надо найти прогибы плиты и найти её внутренние силовые факторы, необходимые для оценки прочности плиты. Важность этой задачи состоит в том, что прямоугольные плиты – основной строительный элемент океанских лайнеров. Другой пример: тонкая прямоугольная пластинка, к сторонам которой приложены некоторые нагрузки, действующие в ее плоскости. Надо выполнить прочностной расчёт пластинки.
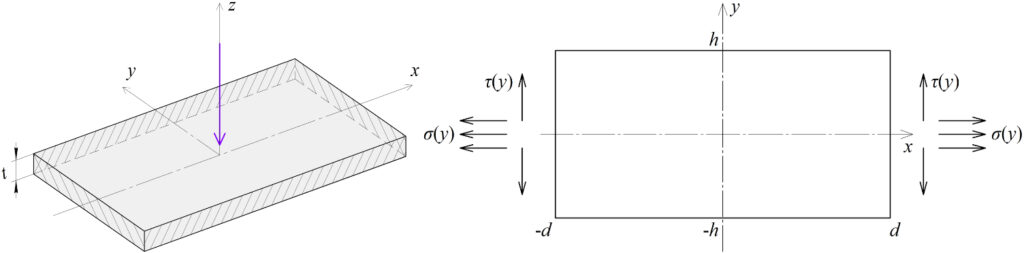
Тонкие пластины – основной строительный элемент, используемый при создании авиационной и ракетной техники. Точные решения этих задач неизвестны, т. е. у инженеров нет готовых формул (за исключением тех, что основаны на приближенных теориях) для решения этих задач. При этом следует учесть, что рассмотренные примеры – это лишь некоторая идеализация: условия крепления плит и пластин, их форма и внешние нагрузки на практике могут быть значительно сложнее. Например, часть контура прямоугольника (не важно, это плита или плоская пластина) может быть защемлена, а другая часть – свободна (так называемые смешанные задачи, точных решений для которых нет); нагрузка может действовать не только по контуру прямоугольника, но и внутри него (неоднородные задачи теории упругости, общих решений для которых нет); прямоугольник может быть нагрет (точных решений термоупругих задач для прямоугольника нет); пластины могут иметь всевозможные ребра жёсткости (примеров точных решений и общей теории точных решений нет). Все сказанное относится и к областям других канонических форм: треугольник, трапеция (в косоугольной системе координат), часть сектора, часть кольца (в полярной системе координат), а также к областям, склеенным из канонических.
С математической точки зрения суть бигармонической проблемы заключается в следующем. Рассмотрим ее опять на примере прямоугольной области. Методом разделения переменных краевая задача приводится к разложениям граничных функций, заданных на двух противоположных сторонах прямоугольника, в ряды по так называемым собственным функциям Папковича–Фадля, которые точно удовлетворяют однородным граничным условиям на двух других сторонах прямоугольника. Эти функции на рубеже 30–40-х годов впервые (независимо) использовались этими учёными для приближенных решений некоторых инженерных задач. Проблема состоит в том, что невозможно, опираясь на классические методы теории базиса функций, определить в явном виде коэффициенты разложений по этим функциям. Сами функции комплекснозначны и достаточно сложно устроены, а приближенные решения, построенные с их использованием, плохо сходятся к граничным функциям. По этим причинам они не получили широкого распространения при решении конкретных задач. Важнейшим результатом этого времени стало соотношение ортогональности, которому удовлетворяют собственные функции Папковича–Фадля, установленное П.Ф. Папковичем в 1940 г. (позже выяснилось, что оно было известно за несколько десятилетий до него, правда, в другой форме). Соотношение ортогональности Папковича послужило толчком к небывалому интересу к собственным функциям Папковича–Фадля в надежде найти точное решение бигармонической проблемы для прямоугольника. К середине 60-х годов в СССР сформировалось несколько групп учёных, объединявших профессиональных математиков и механиков вокруг этой проблемы. Однако ни одного примера точных решений так и не было построено. Интерес к точным решениям стал падать, а в постперестроечное время он практически исчез. И не только на территории бывшего СССР, но и вообще в мире. Этому есть несколько объяснений, одно из которых – крушение отечественных механико-математических школ.
Вопрос о том, что же понимать под точным решением, периодически всплывает на страницах научных изданий. Между тем ответ на него, наверное, до середины 80-х годов был хорошо известен: если решение не выражается через элементарные функции, то точным называется решение в рядах по тем или иным системам собственных функций рассматриваемой краевой задачи, коэффициенты которых определяются в явном виде, например, как интегралы Фурье в известных периодических решениях теории упругости. Если коэффициенты разложений определяются из бесконечных систем алгебраических уравнений, то такое решение не является точным. В рамках этого определения никакие численные решения не могут называться точными.
В основе точных решений классических краевых задач теории упругости в конечных областях с сингулярной границей лежит теория разложений по собственным функциям Папковича–Фадля, развитая в работах коллектива авторов (Коваленко М.Д., Меньшова И.В., Кержаев А.П.). Основная идея состоит в том, что к собственным функциям Папковича–Фадля можно построить биортогональные функции, с помощью которых (как в известных решениях Файлона–Рибьера) определяются неизвестные коэффициенты разложений. Теория разложений по собственным функциям Папковича–Фадля базируется на принципиально новом математическом аппарате – теории базиса для собственных функций Папковича–Фадля (базис на римановой поверхности логарифма). Основанием для развития теории разложений по собственным функциям Папковича–Фадля послужили работы А.Ф. Леонтьева и Ю.Ф. Коробейника по теории экспонент с комплексными показателями, фундаментальная работа А. Пфлюгера по преобразованию Бореля на римановой поверхности логарифма, а также взгляды Д.И. Шермана на понимание им физического смысла точного решения в конечной области с угловыми точками границы.
Основные результаты, полученные авторами:
1. Построены точные решения различных краевых задач теории упругости (основных, смешанных, неоднородных, температурных, с разрывами сплошности и т. д.) в декартовой системе координат, в частности, в полуполосе и прямоугольнике. Наработки различной степени завершённости имеются также по теории разложений по собственным функциям Папковича–Фадля в полярной и косоугольной системах координат.
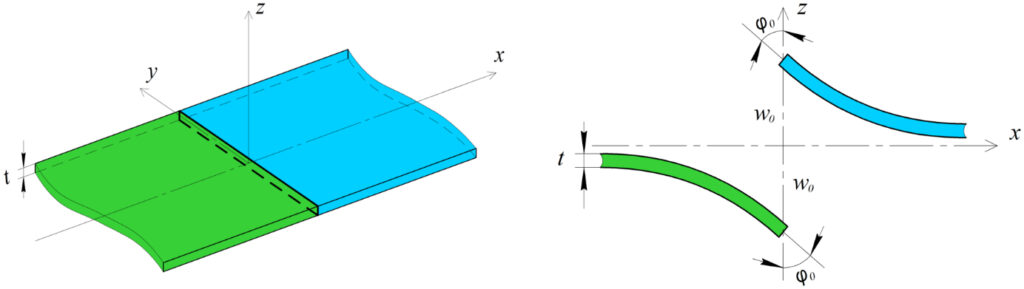
2. Разработана математическая теория остаточных напряжений, которая стала важнейшим следствием решения бигармонической проблемы, имеющим фундаментальное прикладное значение, в частности, в механике горных пород. Отметим несколько признаков, свидетельствующих о наличии остаточных напряжений в какой-либо конечной плоской области: 1) знакопеременность напряжений, являющаяся следствием их самоуравновешенности; 2) фрагменты области, образовавшиеся вследствие её разделения и сброса остаточных напряжений, перемещаются и поворачиваются как абсолютно жёсткие; 3) их невозможно сложить вновь по поверхностям разрыва без зазоров.
Основные публикации
1. Kovalenko M.D., Menshova I.V., Kerzhaev A.P., Yu G. An inhomogeneous problem for an elastic half-strip: An exact solution // Mathematics and Mechanics of Solids, 2021. DOI: 10.1177/1081286521996418.
2. Kovalenko M.D., Menshova I.V., Kerzhaev A.P., Yu G. Expansions in terms of Papkovich–Fadle eigenfunctions in the problem for a half-strip with stiffeners // Zeitschrift für Angewandte Mathematik und Mechanik, 2021. DOI: 10.1002/zamm.202000093.
3. Kovalenko M.D., Menshova I.V., Kerzhaev A.P., Yu G. A boundary value problem in the theory of elasticity for a rectangle: exact solutions // Zeitschrift für angewandte Mathematik und Physik, 2020, vol. 71, no. 6, art. 199. DOI: 10.1007/s00033-020-01425-2.
4. Matrosov A.V., Kovalenko M.D., Menshova I.V., Kerzhaev A.P. Method of initial functions and integral Fourier transform in some problems of the theory of elasticity // Zeitschrift für angewandte Mathematik und Physik, 2020, vol. 71, no. 1, art. 24. DOI: 10.1007/s00033-019-1247-3.
5. Коваленко М.Д., Меньшова И.В., Кержаев А.П., Yu G. Неоднородная задача теории упругости в полуполосе. Точное решение // Известия Российской академии наук. Механика твердого тела. 2020, № 6, с. 33–39. DOI: 10.31857/S0572329920060094.
6. Kovalenko M.D., Abrukov D.A., Menshova I.V., Kerzhaev A.P., Yu G. Exact solutions of boundary value problems in the theory of plate bending in a half-strip: basics of the theory // Zeitschrift für angewandte Mathematik und Physik, 2019, vol. 70, no. 4, art. 98. DOI: 10.1007/s00033-019-1139-6.
7. Kovalenko M.D., Menshova I.V., Kerzhaev A.P. On the exact solutions of the biharmonic problem of the theory of elasticity in a half-strip // Zeitschrift für angewandte Mathematik und Physik, 2018, vol. 69, no. 5, art. 121. DOI: 10.1007/s00033-018-1013-y.
8. Kovalenko M.D., Menshova I.V., Kerzhaev A.P., Guangming Yu. Mixed boundary value problems in the theory of elasticity in an infinite strip // Acta Mechanica, 2018, vol. 229, no. 11, pp. 4339–4356. DOI: 10.1007/s00707-018-2244-x.
9. Kerzhaev A.P., Kovalenko M.D., Menshova I.V. Borel transform in the class W of quasi-entire functions // Complex Analysis and Operator Theory, 2018, vol. 12, no. 3, pp. 571–587. DOI: 10.1007/s11785-017-0643-y.
10. Себряков Г.Г., Коваленко М.Д., Меньшова И.В., Шуляковская Т.Д. Нечетно-симметричная краевая задача изгиба полуполосы с продольными ребрами жесткости. Биортогональные системы функций и разложения Лагранжа // Доклады Академии наук. 2016. Т. 468, № 3. С. 280–284. DOI: 10.7868/S0869565216150123.

