Солнечный цикл, составляющий примерно 11 лет, является основной периодичностью в амплитуде различных солнечных и геомагнитных индексов. Согласно современной теории, происхождение солнечного цикла связано со свойствами солнечного динамо, а длина цикла определяется меридиональной циркуляцией в зоне конвекции.
Успехи гелиосейсмологии позволили восстановить скорости меридионального потока в последних двух солнечных циклах 23-24, однако краткость этих восстановлений по времени и значительная неточность метода на глубине вызвали научную дискуссию о действительной структуре меридионального потока и ее связи с солнечным циклом. В сложившихся условиях, когда прямые наблюдения недоступны, а физические модели магнитного гидродинамо существенно зависят от профиля скоростей меридионального потока, мы применяем математическое моделирование и решаем обратную задачу по восстановлению долговременных свойств меридиональной циркуляции.
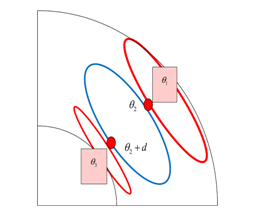
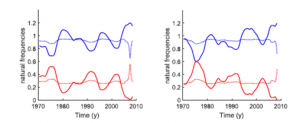
Конкретная модель, на основе которой проводится решение обратной задачи, представляет собой цепочку из трех нелинейно связанных осцилляторов, представляющих циркуляционные ячейки меридионального потока, фазовая эволюция которых описывается уравнениями Курамото. В отличие от классической модели Курамото, предполагается наличие фазовой разницы между точками взаимодействия среднего осциллятора с верхним и нижним (Рис.1). Благодаря этому, эта крайне простая модель отчасти воспроизводит свойства более сложных Курамотовских систем, включающих притягивающие и отталкивающие осцилляторы. В работе исследуется роль фазовой задержки в решении обратной задачи по восстановлению скоростей верхнего и нижнего осцилляторов, определяется ее связь с коэффициентом связи и восстанавливаются скорости меридионального потока при различных значениях коэффициента связи. Показано, что высокая вариативность скоростей меридионального потока, наблюдаемая в гелиосейсмологии соответствует более высокой связи между циркуляционными ячейками и меньшей фазовой задержке (Рис.2, сплошная линия)
Работа опубликована в статье: Elena Blanter, Mikhail Shnirman (2020) Inverse Problem in the Kuramoto Model with a Phase Lag: Application to the Sun, International Journal of Bifurcation and Chaos, Vol. 30, No. 12, 2050165 (15 pages) DOI: 10.1142/S0218127420501655.

