Автор: Новиков Р.Г.
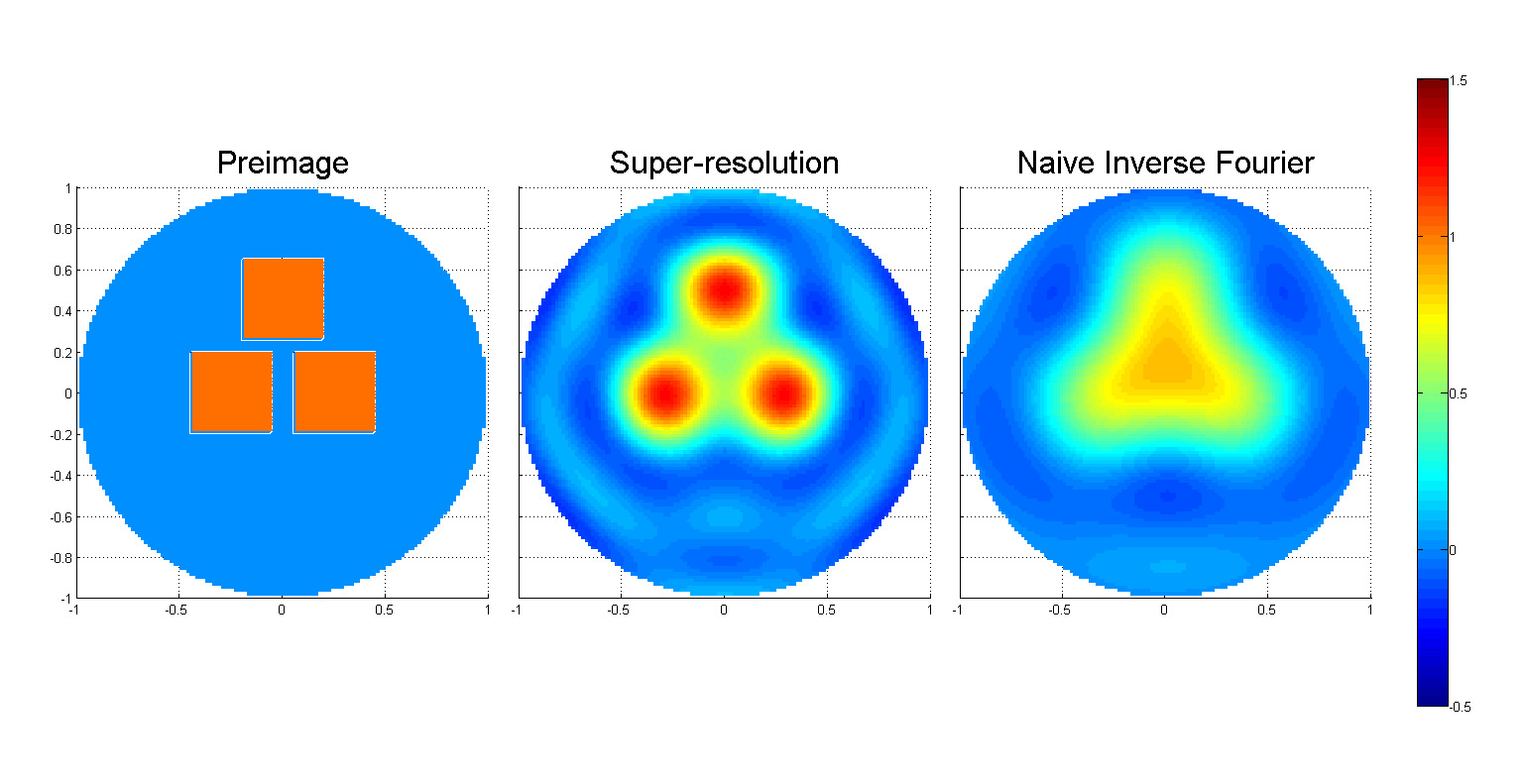
Результатом работ [1] и [2] является существенное развитие теоретических и численных методов восстановления функции с компактным носителем на R^d по её преобразованию Фурье, ограниченному на шар B_r фиксированного радиуса r. В частности, работа [1] даёт новые формулы для такого восстановления. Для одномерного случая эти формулы основаны на теории вытянутых сфероидальных волновых функций. В многомерном случае эти формулы также включают обращение преобразования Радона. При этом численная реализация формул из [1] дана в [2]. В частности, полученные результаты дают сверхразрешающее восстановление, то есть позволяют восстанавливать детали за дифракционным пределом, то есть детали размера меньше чем π/r, где r это радиус шара упомянутого выше.
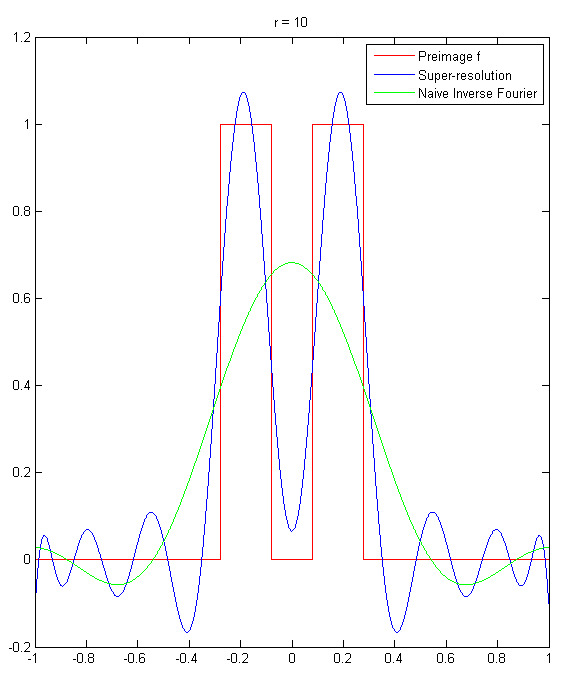
Рисунок 1 иллюстрирует такое сверхразрешающее восстановление в одномерном случае d=1. Рисунок 2 иллюстрирует такое сверхразрешающее восстановление в двумерном случае d=2. Необходимо отметить, что исследования работ [1], [2] по преобрзованию Фурье допускают потенциальные приложения не только к анализу сейсмических данных, но вообще говоря, ко всем областям физики, где возникает преобразование Фурье.
Результаты данного исследования докладывались на научный семинарах Института. Подробнее можно узнать по ссылке.
Источники:
[1] M. Isaev, R.G. Novikov, Reconstruction from the Fourier transform on the ball via prolate spheroidal wave functions, Journal de Mathématiques Pures et Appliquées 163 (July), 318-333 (2022). DOI: 10.1016/j.matpur.2022.05.008
[2] M. Isaev, R.G. Novikov, G.V. Sabinin, Numerical reconstruction from the Fourier transform on the ball using prolate spheroidal wave functions, Inverse Problems 38(10), 105002 (2022). DOI: 10.1088/1361-6420/ac87cb

